Por cuestiones que no vienen al caso, alguien me planteó un problema de nesting 2D que no he podido quitarme de la cabeza y que finalmente ha ocupado algunas de mis madrugadas. Nesting 2D sobre chapas metálicas. El problema involucra varias cosas que me apasionan: geometría, optimización y pide a gritos inteligencia artificial. Así que me puse manos a la obra para desarrollar un prototipo académico. Comentaré aquí los detalles que me han parecido más interesantes, aunque ha habido mucho más detrás. Espero que sea de vuestro interés
- Objetivo
- Lenguajes
- LA GEOMETRÍA: No-Fit Polygon y la suma de Minkowski
- IA: algoritmos genéticos
- Resultados
Objetivo
Uno de los retos más interesantes en fabricación digital es aprovechar la chapa al máximo. Todos sabemos que, en teoría, “solo hay que colocar las piezas lo más juntas posible”. En la práctica, eso significa adentrarse en uno de los problemas más complejos de la optimización geométrica: el nesting. Cuando además cada pieza puede tener agujeros, geometrías libres, múltiples rotaciones posibles y distintas cantidades… la cosa se pone seria. Es un problema habitual también en textil, aunque en ese caso el planteamiento cambia un poco por no ser chapas fijas sino una tela continua.
En mi caso, quería un motor que, a partir de un listado de ficheros DXF donde vienen definidas las piezas, y el número de unidades de cada pieza, fuera capaz de generar automáticamente una propuesta de corte: cuántas chapas se necesitan y dónde debe colocarse exactamente cada pieza. Quería aplicar técnicas de nesting como No-Fit Polygons, búsqueda local, algoritmos genéticos y heurísticas específicas del dominio.
Este texto resume algunas de las claves de cómo funciona por dentro el motor que he construido. Su estructura general y los criterios de optimización aunque es verdad que la magia siempre está en los detalles y no es mi intención aquí entrar en detalles del código.
Lenguajes
Python como “front-end” y procesador de CAD
Antes de pensar en colocar piezas, hace falta asegurarse de que las formas están limpias. Los DXF pueden venir con arcos, polilíneas abiertas, pequeñas incoherencias y orientaciones inconsistentes. Por eso la primera fase del sistema la hace Python: lee los DXF, reconstruye contornos cerrados con shapely, simplifica ligeramente, normaliza orientación (contorno exterior en sentido antihorario, agujeros en sentido horario) y genera un archivo problem_data.json con geometría ya adecuada para el motor de nesting. Además, se tienen en cuenta las cantidades: si una pieza aparece 4 veces en el input, el motor recibirá 4 copias independientes. Hay que tener mucho cuidado con el sentido horario y antihorario porque depende de la programación puedes terminar confundiendo lo sólido con los huecos. Os aseguro que he tenido peleas desesperante con eso.
Esta fase es cómoda en Python, donde la I/O de DXF y la manipulación geométrica de alto nivel resultan mucho más ágiles. También para la visualización de los resultados. Pero para el trabajo duro que requiere mucha computación es mejor que C++ tome el relevo.
El motor en C++: máxima velocidad para cálculos pesados
Una vez normalizadas las piezas, el trabajo serio sucede en C++. Aquí se calcula todo el nesting: NFPs, uniones de polígonos, selección de posiciones, evaluaciones del algoritmo genético, etc.
La decisión técnica es clara: estos cálculos son demasiado pesados para depender solo de Python. C++ permite trabajar a nivel de entero con la librería Clipper2, que aporta robustez y velocidad para todas las booleanas de polígonos. Además, el uso de OpenMP permite paralelizar varias partes del algoritmo (evaluación de candidatos, mutaciones, generación de población…), algo muy beneficioso cuando evaluamos cientos o miles de soluciones en cada generación.
LA GEOMETRÍA: No-Fit Polygon y la suma de Minkowski
Una de las herramientas más potentes -y a la vez menos intuitivas cuando uno la encuentra por primera vez- en problemas de nesting es el No-Fit Polygon (NFP). Puede ser la diferencia entre un nesting ingenuo y uno realmente competente. En esencia, el NFP describe todas las posiciones en las que una pieza colisiona con otra. No se calcula probando puntos ni empujando polígonos entre sí, sino mediante una transformación geométrica preciosa: la suma de Minkowski entre el contorno de la pieza fija y la versión reflejada de la pieza móvil.
Cómo se construye un NFP (explicado sin fórmulas)
- Reflejamos la pieza móvil alrededor del origen.
Esto convierte la relación “distancia entre formas” en una relación equivalente a desplazar un único polígono. - Realizamos la suma de Minkowski entre el contorno de la pieza fija y la pieza móvil reflejada.
- La suma de Minkowski crea una nueva región que representa exactamente:
todas las posiciones donde el origen de la pieza móvil provocaría colisión con la pieza fija. - El resultado suele consistir en uno o varios contornos (a veces con huecos) que se unen y simplifican.
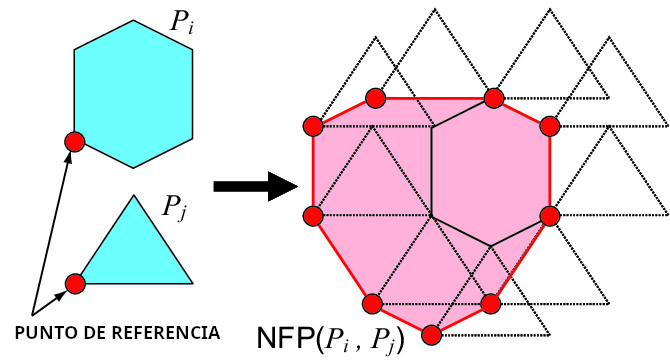
Ese conjunto de contornos es el NFP. Cualquier punto dentro de esa región está prohibido; cualquier punto fuera, es válido.
Cálculo pieza a pieza y por rotación
En un nesting real hay decenas o cientos de piezas, cada una potencialmente con varias rotaciones discretizadas. Por eso el motor calcula todos los NFP necesarios de forma sistemática para cada pieza fija con su rotación correspondiente frente a cada pieza móvil con su rotación correspondiente. Se calcula una vez y se cachea. Esto es imprescindible: el mismo NFP se reutiliza decenas o cientos de veces durante el proceso de colocación.
Coste del cálculo: orden aproximado
El coste de generar un NFP mediante Minkowski depende del número de vértices de ambas piezas. De forma aproximada, si n es el número de vértices de la pieza fija y m el de la móvil:
- Suma de Minkowski: suele escalar en el orden de
O(n · m) en su versión convencional (Clipper2 usa un algoritmo optimizado, pero esta es una estimación razonable). - Unión de contornos resultantes: operación más costosa, típicamente
O(k log k), donde k es el número total de vértices combinados. - Por último, se aplica una validación híbrida mediante point-in-polygon para eliminar falsos huecos que a veces aparecen tras las uniones de contornos. Esta comprobación utiliza el método clásico del rayo horizontal (ray casting): se lanza un rayo desde el punto de prueba y se cuenta cuántas veces cruza el contorno. Es una operación de orden O(N) sobre los vértices del polígono, extremadamente rápida, lo que permite filtrar huecos incorrectos sin penalizar el rendimiento global del motor.
En la práctica, para piezas con pocos agujeros y geometrías moderadas, estos cálculos tardan milisegundos, pero si se repitieran miles de veces serían prohibitivos. Por eso el cache es absolutamente esencial.
El proceso completo NFP
Cada vez que intento colocar una pieza en una chapa, lo que hago es:
- Trasladar todos los NFP relevantes según la posición de las piezas ya colocadas.
- Unirlos todos en un único contorno global (esto es lo que más tiempo cuesta proporcionalmente).
- Restarlo a la región libre de la chapa para obtener todas las posiciones válidas.
La unión global es más costosa que el Minkowski individual, pero solo se hace una vez por colocación, el número de piezas ya colocadas no suele ser brutalmente grande y el filtrado previo con bounding boxes evita juntar NFPs que no pueden influir en la región actual.
Por qué NFP es tan eficiente comparado con métodos básicos
Otros métodos clásicos para evitar colisiones suelen basarse en probar muchos puntos y verificar intersecciones, desplazar gradualmente una pieza y comprobar solapamientos, utilizar cuadrículas discretas o mapas de ocupación, o hacer collision checks entre polígonos en bucles anidados. Todos esos métodos son O(n) o O(n log n) cada vez que se prueba una posición, y además requieren probar muchísimas posiciones.
El NFP, en cambio, precomputa toda la geometría de colisión de una vez, por pieza y rotación. Después, comprobar si una posición es válida es trivial (¿está fuera del NFP?). Obtener todas las posiciones válidas dentro de una chapa se reduce a una operación booleana entre polígonos. Las mejores posiciones (bottom-left / left-bottom) se obtienen explorando directamente la frontera de la región válida, no escaneando el plano. Y eso hace el motor infinitamente más escalable.
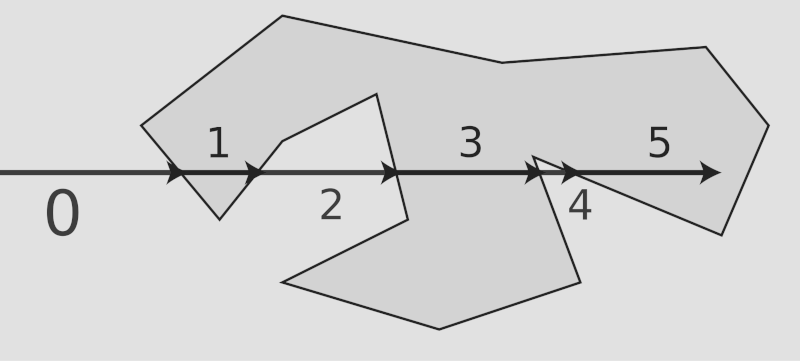
Encontrar la mejor posición: Bottom-Left mejorado
A partir de la región libre resultante (la chapa menos los NFP trasladados), el motor evalúa dónde colocar la pieza. La estrategia clásica sería un Bottom-Left, que intenta encontrar la coordenada más baja y más a la izquierda posible. Pero en mi implementación hay una variante interesante: también se evalúa la estrategia opuesta, Left-Bottom, para después elegir en cada caso la estrategia ganadora. Y si ambas producen posiciones de calidad parecida, se toma una decisión basada en un criterio de contacto.
Esta medida de contacto inflando ligeramente la geometría permite cuantificar qué posición “abraza” mejor a las piezas ya colocadas, lo que tiende a producir un nesting más compacto. Es un pequeño detalle, pero ese tipo de heurísticas ayudan a aprovechar más cada chapa.
IA: algoritmos genéticos
Algoritmo Greedy inicial
Antes de arrancar el algoritmo genético, el sistema genera una primera solución con una estrategia Greedy sencilla: ordenar las piezas por área (las grandes primero) y colocarlas en ese orden con rotación inicial cero. Aunque esta solución no suele ser óptima, sirve como individuo semilla razonablemente bueno para arrancar la evolución. El propio algoritmo ya reordena las piezas porque va colocándolas en la primera chapa que cabe. Según se van llenando, las pequeñas pasan a estar antes que otras grandes que no habían cabido en una chapa ya bastante llena. Es muy sencillo pero sorprendentemente eficaz para un comienzo.
El algoritmo genético: prioridad, rotación y reinicio adaptativo
Aunque hoy en día todo parece girar en torno al machine learning -y es cierto que problemas como este podrían abordarse con técnicas modernas como aprendizaje por refuerzo, búsqueda Monte Carlo guiada por redes neuronales o incluso modelos neuroevolutivos diferenciables– para este proyecto he preferido recurrir a una herramienta old school de la inteligencia artificial que sigue siendo extraordinariamente eficaz en problemas combinatorios: los algoritmos genéticos. Para quien no esté familiarizado con ellos, un GA es un método inspirado en la evolución biológica: se mantiene una población de soluciones candidatas, cada una codificada como un “ADN” abstracto; esas soluciones se evalúan según una función de fitness, se seleccionan las mejores, se recombinan entre sí y se someten a pequeñas mutaciones. Generación tras generación, el proceso explora el espacio de soluciones buscando combinaciones cada vez más adaptadas. Es una técnica robusta, flexible y muy competitiva cuando el espacio de búsqueda es inmenso y no existe una fórmula directa para encontrar la solución óptima.
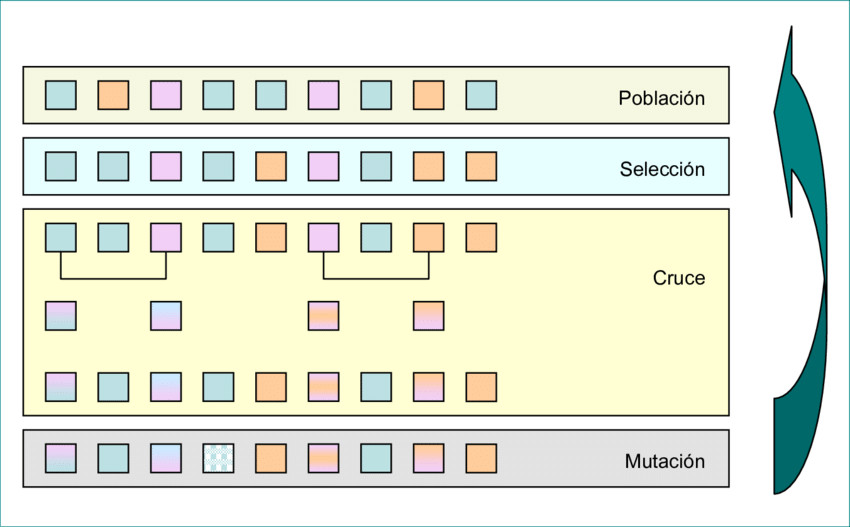
La representación genética del problema tiene dos componentes por pieza que definen dónde y cómo colocamos cada pieza:
- La rotación escogida (un índice entre todas las rotaciones precalculadas).
- Una prioridad, que influye en el orden de colocación. Al ordenar las piezas por este valor se induce una permutación, y esa permutación es la clave de la estructura final de la solución.
Hay que tener en cuenta que la combinatoria que surgiría de probar todas las posibles rotaciones y prioridades sería astronómica y completamente inabordable desde un punto de vista computacional, incluso restringiendo mucho el espacio de búsqueda. Es aquí donde los algoritmos genéticos -o algunas de las técnicas de IA más modernas, aunque no necesariamente superiores- permiten explorar soluciones de forma inteligente y converger hacia resultados realmente buenos, aunque no garanticen encontrar el óptimo absoluto. Y, en cualquier caso, buscar ese óptimo constituiría un problema NP-difícil, por lo que no resulta realista pretender resolverlo de forma exacta en tiempos razonables.
El sistema arranca con una población inicial donde el mejor individuo es el resultado del Greedy. El resto se generan con rotaciones y prioridades aleatorias, incluyendo una fracción que solo usa rotaciones ortogonales para fomentar la diversidad estructural. Durante cada generación se aplica selección por torneo y un cruce que preserva bloques ordenados de prioridades dentro de una ventana. No uso “Smart Order Crossover” en sentido estricto; lo que utilizo es un cruce por rango que mantiene subórdenes útiles sin imponer una semántica fuerte de permutación clásica. Es una adaptación práctica que funciona muy bien para este tipo de problemas híbridos.
Para visualizarlo mejor, puede imaginarse como cortar un trozo de pastel. En vez de seleccionar ingredientes sueltos y mezclarlos al azar, lo que hago es cortar una porción entera del pastel del padre 1 (un bloque de piezas que ya funcionan bien juntas) y colocarla directamente en el hijo. El resto del pastel se rellena con material del padre 2. Esto tiene una consecuencia muy natural: si dos o más piezas ya estaban juntas y encajaban bien en una chapa, probablemente es mejor moverlas juntas a la siguiente generación que separarlas. Mantener ese suborden favorece que patrones útiles de empaquetado sobrevivan, mientras que el crossover tradicional de permutaciones rompe con mucha más facilidad esos grupos.
Las mutaciones tienen dos focos:
- Mutación de rotación, con tres comportamientos:
- 60%: acercarse a una rotación ortogonal (muy efectivo en chapas rectangulares).
- 25%: afinar con un pequeño paso angular arriba/abajo.
- 15%: cambiar completamente a una rotación aleatoria.
- 60%: acercarse a una rotación ortogonal (muy efectivo en chapas rectangulares).
- Mutación de prioridad, que introduce pequeñas perturbaciones o realiza swaps puntuales entre piezas, lo que puede abrir nuevos patrones de ocupación en una chapa.
Además, si pasan demasiadas generaciones sin mejorar la mejor solución, se activa un reinicio adaptativo: se conserva el mejor individuo y se regenera el resto de la población desde ruido controlado. Esto recuerda a un Micro-GA, pero no lo es exactamente; es una mezcla entre restart strategies y diversificación programada. El efecto práctico es bueno: evita que la búsqueda se estanque en óptimos locales. Además, una estrategia similar a Micro-GA funciona bien para poblaciones pequeñas, y dado el coste de calcular cada indivíduo no conviene que tengamos demasiados.
Búsqueda local: afinar el individuo campeón
Si se activa la búsqueda local, el mejor individuo de cada generación se somete a una fase adicional donde se generan variaciones específicas. Otra forma de afinar es mutar especialmente las piezas de la última chapa. Tanto una opción como la otra están parametrizada para usarlas o no (suele mejorar un poco el resultado pero también ralentiza un poco y no siempre es necesario). Esta forma de búsqueda local estocástica se parece a un hill climbing dirigido: explora la vecindad de forma inteligente sin sacrificar diversidad.
Heurísticas adicionales: adherencia y lookback
Hay dos heurísticas que ayudan más de lo que podría parecer:
- Adherencia (contacto): cuando dos posiciones posibles son prácticamente equivalentes en distancia al origen, se prioriza la que tiene mayor zona de contacto con el material ya colocado. En la práctica genera patrones más compactos.
- Lookback limitado: cuando se coloca una pieza grande, el motor no recorre desde la primera chapa hacia adelante, sino que empieza directamente por las chapas más recientes. En los casos reales esto tiene muchísimo sentido: intentar encajar una pieza grande en una chapa que ya está casi llena es perder tiempo.
Cómo se evalúa una solución: la fórmula de fitness
La calidad de una solución se mide con una función que combina dos ideas:
- Cada chapa aporta un valor proporcional a su eficiencia de uso, pero elevado al cuadrado. Esta elección refuerza que las chapas muy bien llenas son mucho más valiosas que repartir huecos uniformemente.
- Se penaliza el uso de chapas por encima del número “ideal” (definido como el área total de todas las piezas dividido por el área de una chapa).
En esencia, se favorece usar pocas chapas y que estén lo más llenas posible.
Resultados
Tras ejecutar el algoritmo genético durante las generaciones configuradas, el motor genera un solution.json que contiene el número total de chapas usadas, la eficiencia individual de cada chapa, la posición exacta y la rotación de cada pieza y las coordenadas finales de la geometría ya transformada. La visualización se realiza ya de vuelta en Python.
Los resultados que muestro a continuación provienen de dos colecciones de piezas incluidos en los repositorios de referencia de ESICUP, en el ámbito académico del nesting: los conjuntos Jakobs 2 (1996) y Han (1996). ESICUP es el European Special Interest Group on Cutting and Packing, un grupo especializado que coordina investigadores, benchmarks y competiciones sobre problemas de corte, empaquetado y nesting. Muchas de las piezas “estándar” que se usan para comparar algoritmos proceden de allí.
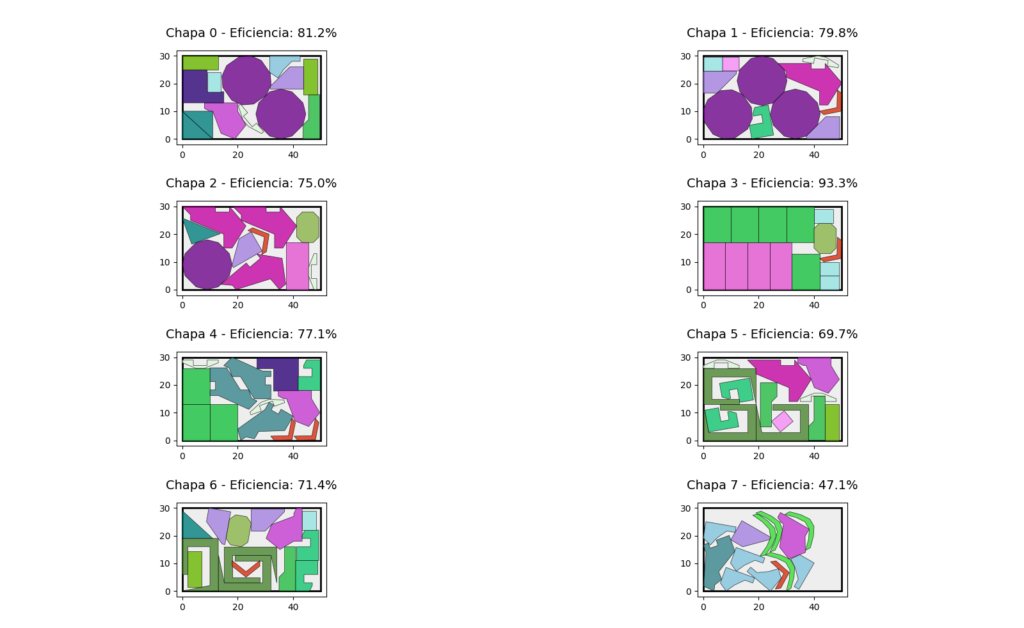
Las piezas de Han son irregulares y rebeldes para el nesting. En el caso concreto del conjunto Jakobs, las piezas son algo más sencillas (aunque es la versión 2 que son más irregulares que la 1), y las he usado para plantear experimentos con muchas unidades y chapas grandes, elevando significativamente la carga computacional. Esto convierte el problema en un buen banco de pruebas: añadir cientos de unidades incrementa drásticamente la combinatoria, y obliga al motor a demostrar realmente su eficacia tanto en optimización geométrica como en eficiencia numérica.
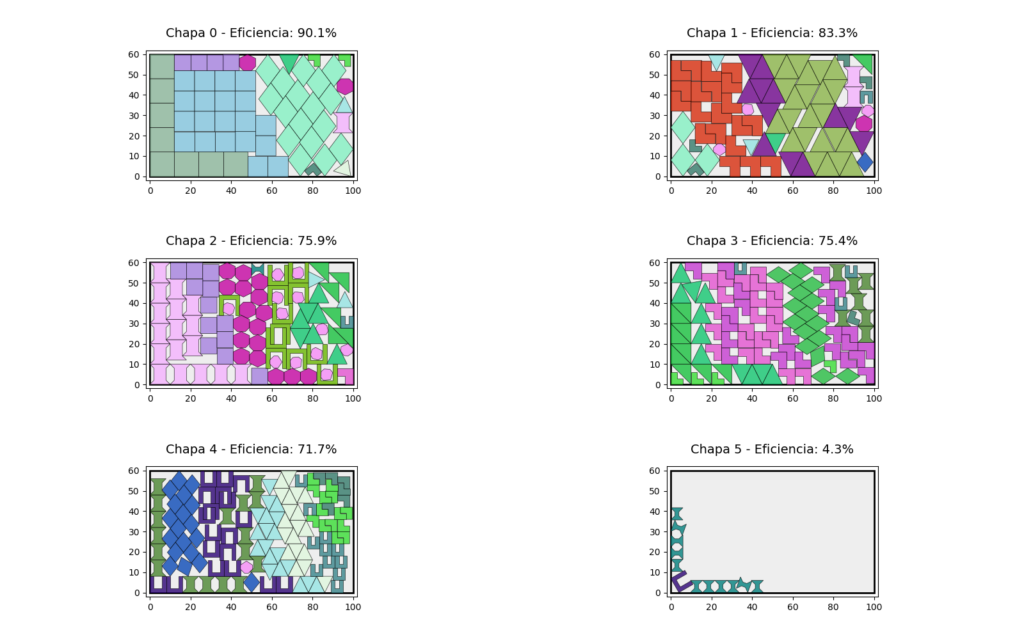
Conviene insistir en que este motor es, ante todo, una versión académica orientada a experimentar con estructuras de datos especializadas, heurísticas de colocación y un algoritmo genético bien adaptado al nesting. En un entorno productivo real sería perfectamente razonable invertir tiempos de cómputo mayores, ejecutar el motor en máquinas más potentes o distribuidas y optimizar aún más partes críticas del pipeline (cachés, paralelización fina, manejo de memoria, etc.). Del mismo modo, el motor no incorpora restricciones específicas de máquinas industriales de corte que suelen requerir reglas adicionales: márgenes mínimos por sensibilidad térmica, distancias entre trayectorias, ordenaciones especiales de entrada/salida, etc. Implementar estas condiciones es perfectamente posible, pero no era el objetivo aquí, porque no cambia demasiado la forma de abordarlo. Además, las colecciones usadas estaban ideadas para strip packing (cinta infinita) con lo que no puedo usar sus benchmarks.
Lo que se buscaba era validar la arquitectura general, comprobar que los cálculos geométricos (NFP, booleanas, bounding strategies) se comportaban bien, y medir cómo las heurísticas y el algoritmo genético conseguían construir soluciones compactas y estables incluso con volúmenes altos de piezas. En ese sentido, los resultados obtenidos muestran que el enfoque es sólido y extensible, y sienta unas muy buenas bases para un motor de nesting plenamente operativo.
¿Próxima parada?
- A) Seguir optimizando este sistema
- B) Empezar otro desde cero con machine learning
